오늘은 Cache의 종류에 대해 알아보자. 우리는 AMAT를 줄이는 방향으로 나아가야 한다. 어떻게 줄일 수 있을까?
AMAT란 무엇인지 모른다면 다음 포스팅을 참고하면 좋다.
2022.03.23 - [내가 하는 전자공학/컴퓨터 구조] - 컴퓨터 구조 AMAT ( Average Memory Access Time, cache 성능 평가 )
컴퓨터 구조 AMAT ( Average Memory Access Time, cache 성능 평가 )
cache의 성능을 어떻게 평가할 것인가에 대한 지표가 AMAT이다. cache는 instruction과 Data가 존재하는데 cache에 cpu가 찾는 데이터가 있다면 이걸 HIT이라고 하고 cache에 없다면 miss라고 한다. 없다면 메인
wpaud16.tistory.com
AMAT = Hit time + Miss rate * Miss penalty
AMAT를 줄이기 위해 단순하게 생각했을 때, cache의 사이즈를 늘리는 것이다. 그렇다면 hit rate가 올라갈 것이다.
하지만 이건 해결책이 못된다. 이유는 cache가 커지면 hit time이 늘어난다. 즉, 데이터를 찾는데 오래 걸린다는 의미다.
다른 방법으로는 어떤 게 있을까
1. Miss Rates를 줄이는 것이다. 그러기 위해서는 cache의 구조를 바꿔야 한다.
2. Miss penalty를 줄이는 것이다.
첫 번째 방법부터 알아보자
cache 구조 ( Reduce Miss Rate )
지금까지 우리는 DM$ 구조를 기준으로 봤는데 캐시의 종류는 DM$ 말고 2-Way set associative, 4-Way set associative, Fully associative와 같이 여러 종류가 있다.
차이점은 간단하다. DM$는 하나의 block에 하나의 Tag, Data가 있다. 그래서 데이터를 찾을 때, 하나의 데이터를 타깃으로 찾았다.
하지만 N-Way set associative와 같은 방법에는 block의 단위가 아니라 Set이라는 집합의 단위로 사용한다. 같은 cache의 사이즈이지만 2-Way이니 2개씩 묶어서 보는 것이다. 하나의 Set을 선택하면 거기에는 2개의 데이터가 존재한다.
나머지도 마찬가지다. DM$를 조금 다르게 보면 1-Way set인 것이다.

그림을 보고 하나하나 어떻게 동작하는지 보자. 아래는 4-Way를 사용한 캐시다.
32bit cpu를 가정하고 16KB cache size에서 block size는 4Byte다. 하나의 way 크기는 16KB / 4 = 4KB이고
이에 entry 개수는 4KB / 4B = 1K = 1024 임을 알 수 있다.

CPU Address의 32bit 중에 block size가 4B이므로 2개 비트를 무시하고 1024이니 10bit를 index 선택에 사용한다.
하나의 index를 선택하면 4개의 데이터가 존재하는데 기존애 있던 Tag와 새로운 Tag가 같은지 연산을 하고 Valid가 1인지 확인하여 or gate에 집어넣는다. 만약 하나라도 1이 있다면 Hit 했다는 의미다.
그리고 4개의 데이터는 MUX를 이용해서 내보는데, 이때 sel 신호는 Hit 신호를 판단할 때 썼던 신호를 쓴다. 위에선 노란색에 해당한다.
이렇게 동작하는 것이 4-Way set associative cache이다.
이게 왜 Miss rate를 줄이는데 도움이 될까? 과학적으로 증명되진 않았지만 확률적으로 보면 Miss rate가 줄어드는 걸 알 수 있다.
같은 index를 가르쳤을 때 DM$는 TAG가 같지 않으면 항상 miss다. 하지만 n-Way set에서는 일단 데이터가 다 채워질 때까지는 똑같이 miss다. 하지만 여러 데이터가 같이 있으니 자연스레 miss rate가 줄어드는 효과가 있다.
LRU ( Least recently used )
그렇다면 cache 데이터가 꽉 차 있는데 새로운 데이터가 들어온다면 (miss) 있던 데이터 중에 어떤 데이터에 덮어씌울까?? 이때 나온 게 LRU이다.
LRU방법은 가장 오래된 데이터 위에 덮어 씌운다. LRU bit를 추가해서 확인한다. 만약 위에서처럼 4 way 라면 몇 bit가 필요할까?? 정답은 5bit이다. 필자는 처음에 2bit만 있으면 될 줄 알았지만, 과거의 데이터를 기억할 수 없기 때문에 2bit는 불가하다.
왜 5bit일까?? 위를 예시로 보면 우리는 네 가지를 기억해야 한다. 수학의 조합으로 보면 쉽다. ㅁㅁㅁㅁ 이렇게 4개의 칸에 0~3에 해당하는 숫자가 들어갈 수 있는 조합은 어떻게 될까? 4!이다. 즉, 24가지가 존재한다. 그래서 4bit면 16가지 밖에 할 수 없으므로 5bit가 필요하다.
만약 8 way라면 어떻게 될까?? 8!이라 너무 많은 bit가 필요하다. 그래서 실제로는 이 방법을 쓰지 않고 Random 하게 선택하여 변경하다.
cache 다중층 (Reduce Miss penalty)
Miss penalty를 줄이는 방법은 cache를 다중층으로 두는 것이다. 반도체 집약 기술이 발전하여 더 작은 단위의 cache를 구현할 수 있게 됐다.
그래서 cache에 L1, L2, L3와 같은 cache가 존재할 수 있다. L1에서 miss가 발생하면 L2로 가고 L2에도 없으면 L3로 간다. 이런 식으로 여러 단계를 거치는 것이다.

cache friendly code
cache를 알면 code를 짤 때도 훨씬 많은 도움을 받을 수 있다.
가령, 반복문에서 2차원 배열을 생성하고 각각의 요소에 2배를 하는 코드를 짜면, 아래와 같이 2가지 버전으로 짤 수 있다. 이 두 가지 중에 어떤 코드가 더 cache를 잘 이용한 것일까?
# 버전1
for (j=0; j<100; j++)
for (i=0; i<5000; i++)
x[i][j] = 2*x[i][j]
# 버전2
for (j=0; i<5000; j++)
for (i=0; j<100; i++)
x[i][j] = 2*x[i][j]
버전 1은 열 ( column )을 고정시키고 행 ( row )을 순차적으로 곱해간다. 그러면 다음과 같은 그림으로 볼 수 있다. 즉, Miss가 많이 발생하는 구조로 동작한다.
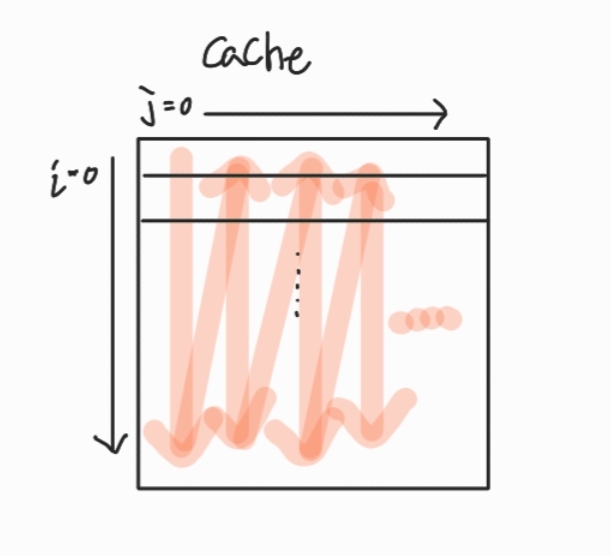

버전 2는 어떨까? 행을 고정시키고 열 방향으로 곱해간다 그러면 다음과 같이 볼 수 있다. 만약 block size가 8B이고 X [10][8]이라면 Miss가 행이 변할 때 빼고는 없다. 즉, Miss의 비율이 줄어든다.
이런 동작을 고려하고 짜면 더욱 좋은 code를 짤 수 있다.




댓글