아래는 내용을 유튜브에 올려놓은 겁니다.
https://www.youtube.com/watch?v=ouSqaaumhvE
보수란 각 자리의 숫자 합이 일정한 값이 되는 것이다. 즉 일정한 값을 만들기 위해 보충해주는 숫자이다. 이런 보수를 왜 쓰냐면 컴퓨터는 뺄셈일 할 수 없고 뎃셈만 할 수 있는데 보수를 이용하면 뺄셈의 역할을 수행할 수 있기 때문이다.
이번엔 10의 보수와 9의 보수와 2의 보수, 1의 보수를 간단히 알아보겠다.
10의 보수를 구하는 방법 & 10의 보수를 이용한 뺄셈
10의 보수란 각 자릿수와 어떤 값을 더해 10을 만들 수 있는 어떤 값을 찾는 것이다. 간단한 방법이 있다.
첫 번째, 0이 아닌 제일 마지막 수를 10에서 뺀다. (자릿수가 올라가기 때문에 10을 뺀다)
두 번째, 나머지 숫자를 9에서 뺀다. (제일 마지막에서 1씩 올라오기 때문에 9를 뺀다)

7이 제일 마지막에 있는 숫자이므로 10에서 뺀다. 그리고 나머지 숫자를 다 9에서 빼면 끝이다.
이번엔 뺄셈을 해보겠다. 결국은 보수를 이용하여 뺄셈을 하는 것이 목표이기 때문에 어떻게 되는지만 알면 된다. 계산은 컴퓨터가 하게 때문이다!
첫 번째, 앞에 있는 값은 그대로 둔다.
두 번째, 뒤에 있는 값은 10의 보수를 취한다
세 번째, 두 수를 더하고 캐리가 발생하면 무시하고 발생하지 않으면 (-) 부호를 붙인다.

실제로 435 - 122 = 313이라는 값이다.
근데 궁금증이 생긴다. 만약 결과 값이 음수라면?? 어떻게 할까?? 정답은 우리가 취해줬던 보수를 다시 취해준다. 그러면 원하는 값이 나온다.
하지만 실제로는 999가 -1이다. 사람이 보기 편하게 하기 위해 다시 보수를 취해주고 -를 붙이는 것이다.

9의 보수 구하는 방법 & 9의 보수를 이용한 뺄셈
9의 보수란 10의 보수와 마 친가지로 각 자릿수의 합이 9를 만드는 값을 찾는 것이다. 10의 보수보다 더 간단하다.
방법은 모든 자릿수를 9에서 뺀다. 10의 보수와 다른 이유는 10의 보수는 자릿수가 올라가기 때문에 제일 끝자리를 10에서 빼는 것이다. 하지만 10진수에서 9는 올라갈 자릿수가 없기 때문에 9를 빼면 된다.

뺄셈은 10의 보수 뺄셈과 유사하다.
첫 번째, 앞에 있는 값은 그대로 둔다.
두 번째, 뒤에 있는 값은 9의 보수를 취한다
세 번째, 두 수를 더하고 캐리가 발생하면 발생한 캐리를 결괏값에 더해준다. 발생하지 않으면 다시 9의 보수를 취하고 (-) 부호를 붙인다.

이렇게 발생한 캐리를 다시 더해준다 10의 보수에서는 캐리를 버렸지만 9의 보수와 1의 보수에서는 그렇지 않다.
2의 보수 구하는 방법 & 2의 보수를 이용한 뺄셈
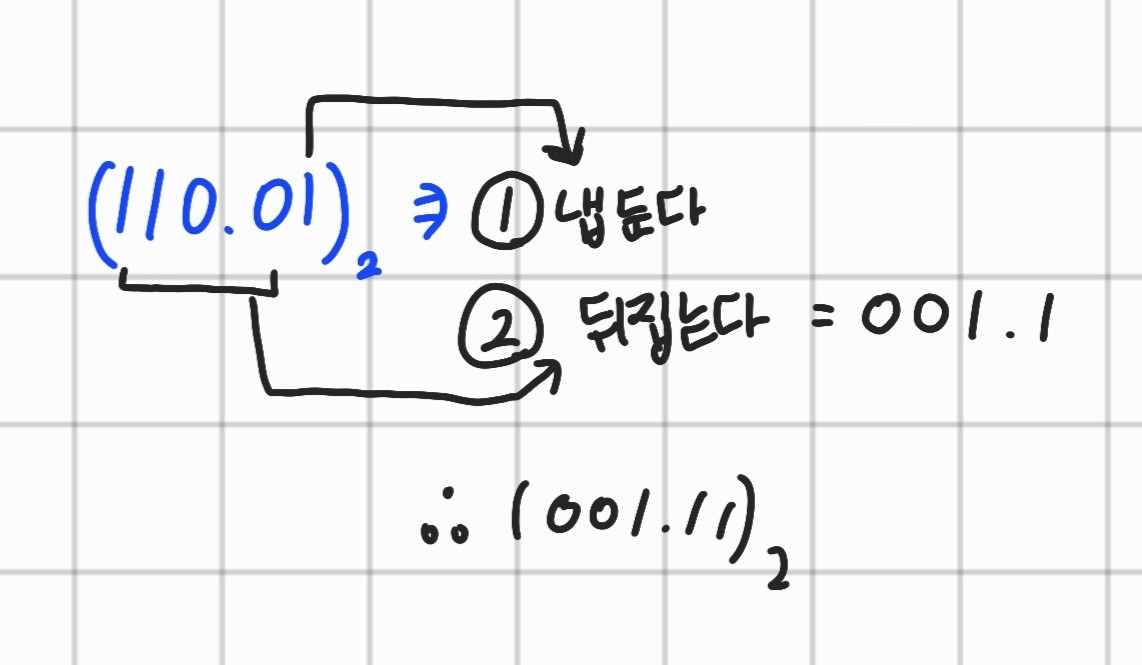
10의 보수와 마찬가지로 2의 보수도 똑같다고 보면 된다. 2의 보수란 각 자릿수의 합이 0이 되면 된다. 2진수이기 때문에 0과 1밖에 없다. 10의 보수와 유사한 방법을 따른다.
첫 번째, 제일 끝수는 내버려 둔다.
두 번째, 나머진 다 뒤집는다.
뒤집는다는 말이 뭔지 잘 모르겠다면 0을 1로, 1을 0으로 바꾼다는 의미다.
이해하기 어렵다면 다른 방법이 있다.
첫 번째, 다 뒤집는다.
두 번째, +1을 한다.
결과적으로 같음을 알 수 있다. 하다보면 두번째 방법이 더 쉽다.
2의 보수를 이용하여 뺄셈을 해보자 방법은 10의 보수와 똑같다.
첫 번째, 앞에 있는 값은 그대로 둔다.
두 번째, 뒤에 있는 값은 2의 보수를 취한다
세 번째, 두 수를 더하고 캐리가 발생하면 무시하고 발생하지 않으면 (-) 부호를 붙인다.
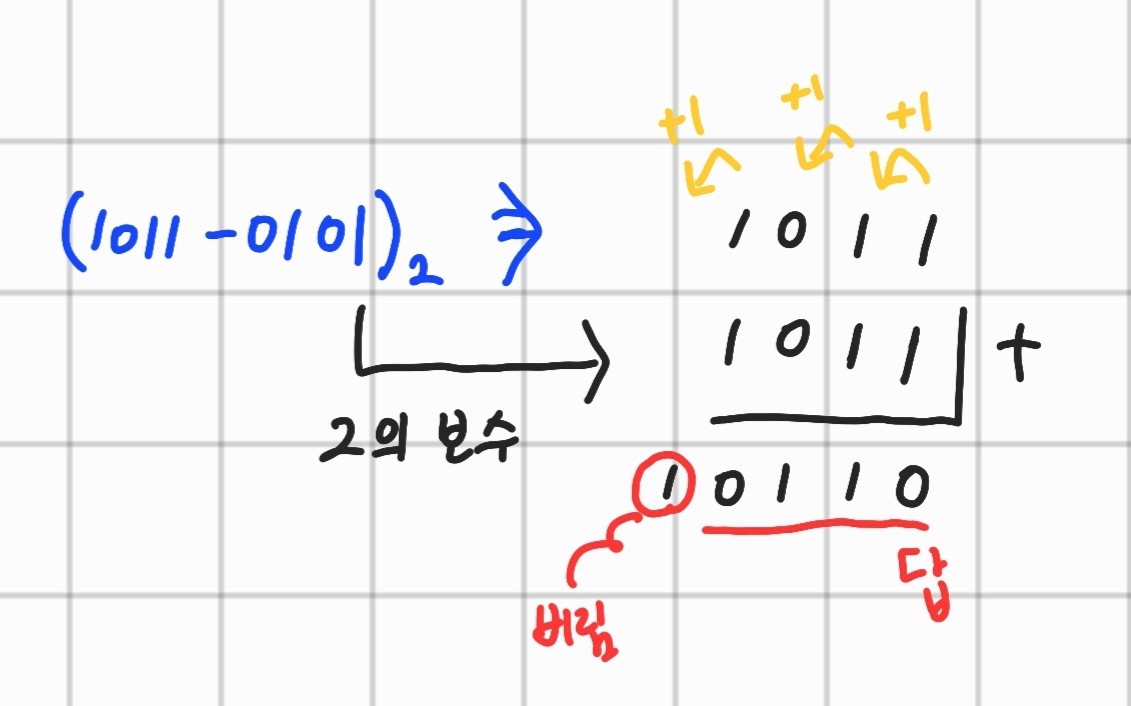
컴퓨터는 이처럼 계산한다. 1011 = 11이고 0101 = 5인데 정답인 0110 은 10진수로 6이다. 올바르게 나온 걸 확인할 수 있다. 만약 음수가 나온다면 어떻게 해야 할까?? 10의 보수에서 본 것처럼 다시 2의 보수를 취하고 (-)를 붙이면 된다.
1의 보수 구하는 방법 & 1의 보수를 이용한 뺄셈
제일 쉽다 그냥 다 뒤집는다.
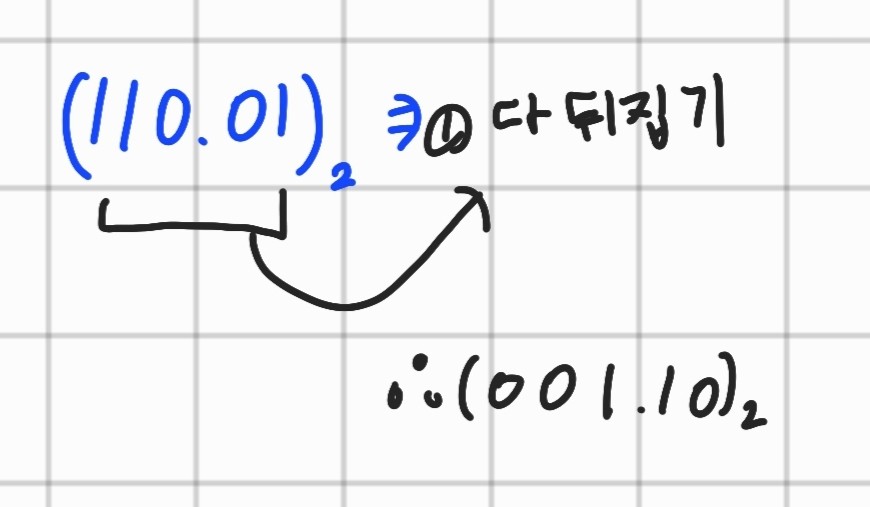
뺄셈은 9의 보수와 똑같다
첫 번째, 앞에 있는 값은 그대로 둔다.
두 번째, 뒤에 있는 값은 1의 보수를 취한다
세 번째, 두 수를 더하고 캐리가 발생하면 발생한 캐리를 결괏값에 더해준다. 발생하지 않으면 다시 1의 보수를 취하고 (-) 부호를 붙인다.
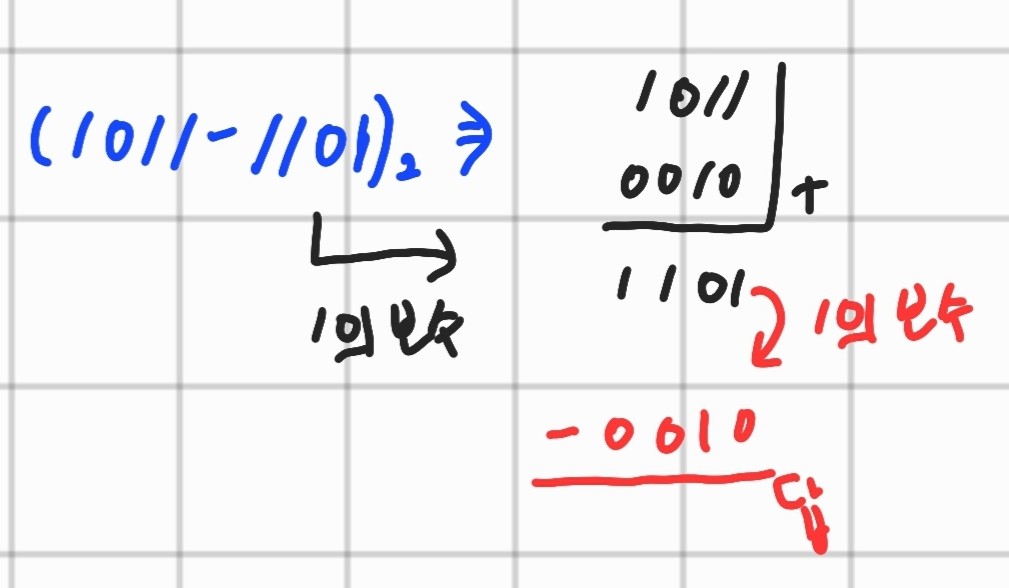
근데 이상하다. -0010을 10진수로 바꾸면 -2로 정답이지만, 컴퓨터는 (-) 음수가 없다고 하지 않았나?? 맞다. 저렇게 계산을 하고 (-)를 붙이는 건 우리가 보기 쉽게 하기 위함이고 컴퓨터는 다른 방식을 취한다.
2진 음수의 표현은 3가지 방식이 있다.
첫 번째, 부호 절댓값 방식
두 번째, 1의 보수 방식
세 번째, 2의 보수 방식
이렇게 총 3가지 방식이 있는데 다음 포스팅에서 각각의 방법을 이용한 연산을 올리겠다.
'반도체 기초 공부 > 논리회로' 카테고리의 다른 글
| 논리회로 상태도(state diagram) (0) | 2022.01.06 |
|---|---|
| 논리회로 조합회로 종류 (반가산기, 전가산기, 반감산기, 전감산기, 멀티플렉서, 디멀티플렉서, 리플 캐리 가산기, 병렬 가감산기, BCD 가산기, 인코더, 디코더) (0) | 2022.01.04 |
| 논리회로 코드 종류 (BCD 코드, 3초과 코드, ASCII 코드, grey 코드) (0) | 2022.01.04 |
| 논리회로 게이트 종류 ( NOT, AND, OR, XOR, NAND, XNOR, NOR ) (0) | 2021.12.29 |
| 논리회로 정보 표현 단위 ( 바이트, 비트, byte, bit) (0) | 2021.09.28 |




댓글