KMeans
KMeans는 중앙점 seed와 개체들 간의 평균 거리를 기준으로 군집을 형성하는 알고리즘을 KMeans 클러스트링이다.
동작 순서는 아래와 같다
1. 지정 클러스터의 수에 맞게 임의로 중심을 지정한다
2. 거리를 기준으로 클러스트링을 한다.
3. 이전 클러스트링 내에서 중심을 새로 지정한다.
4. 바꿔도 군집이 바뀌지 않으면 종료한다.
자세한 설명은 아래 글을 참고하면 좋다.
https://eunsukimme.github.io/ml/2019/12/16/K-Means/
기본적인 KMeans의 동작은 알고 있다고 생각하고, 어떻게 최적의 클러스터 개수를 지정할 수 있을지 알아보자.
두 가지 방법이 있다. 하나씩 알아보자
1. Elbow Method
2. Silhouette Method
Elbow Method
보편적이고 간단하게 사용하는 방법이다. 한국말로 하면 팔꿈치 방법이다. 왜 팔꿈치인지는 후에 알아보자.
구동 원리 또한 간단하다.
방법은 n일 때, 각각의 클러스터 중심에서 클러스터 내의 포인트들의 거리의 제곱합이다. 이게 끝이다. Kmeans에서는 중심을 기준으로 군집을 정하기 때문에 그 중심으로부터 얼마나 떨어져 있냐가 밀집도를 나타낸다.
그러니 합이 최소라면 군집 내에 거리가 가깝게 모여 있다는 의미로 볼 수 있다. 즉, 그때가 바로 제일 이상적인 k이다.
아래와 같은 그래프가 나온다. 라이브러리로는 inertia_를 사용하면 된다.
kmeans = KMeans(n_clusters = k).fit(points)
kmeans.inertia_

하지만 이 방법은"적당한" K를 찾는데 이게 모호하다. 위에선 3인지 4인지 명확하게 알 수 없다. 이를 보안하기 위해 Silhouette Method가 있다.
Silhouette Method
그림을 보고 설명하자면,
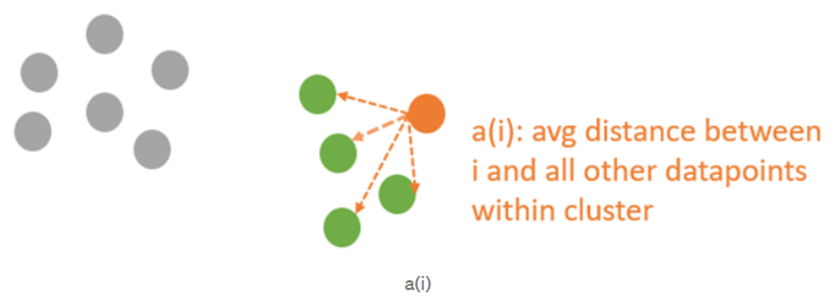


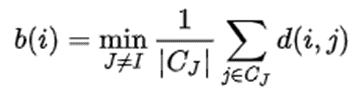
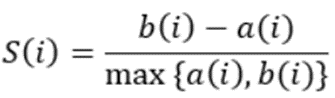
a(i)는 같은 군집에서 다른 포인트들과의 거리 평균을 구한 값이다. (Ci는 군집의 포인트 개수다)
b(i)는 다른 군집에서의 최소 거리 평균을 구한 것이다. 이때 서로 다른 모든 군집과 하는 게 아니라, 가장 가까운 군집과의 거리만 구한다. 이게 하나의 클러스터에 대한 값이다. 만약 여러 클러스터가 있다면 각각의 클러스터의 실루엣 계수를 구해서 평균을 구하면 된다.
실루엣 계수는 -1 ~ +1 사이의 값을 가지며 비교 대상 군집이 있어야 하므로 최소 2개의 군집을 이루어야 한다.
결과적으로 말하면, S(i)의 값이 크다는 건 군집 간의 거리가 멀다는 의미로 잘 군집화 돼 있다고 볼 수 있다.
코드로는 아래와 같이 볼 수 있다. 여기서 points는 데이터 셋을 의미한다.
from sklearn.metrics import silhouette_score
kmeans = KMeans(n_clusters = k).fit(points)
labels = kmeans.labels_
silhouette_score(points, labels, metric = 'euclidean')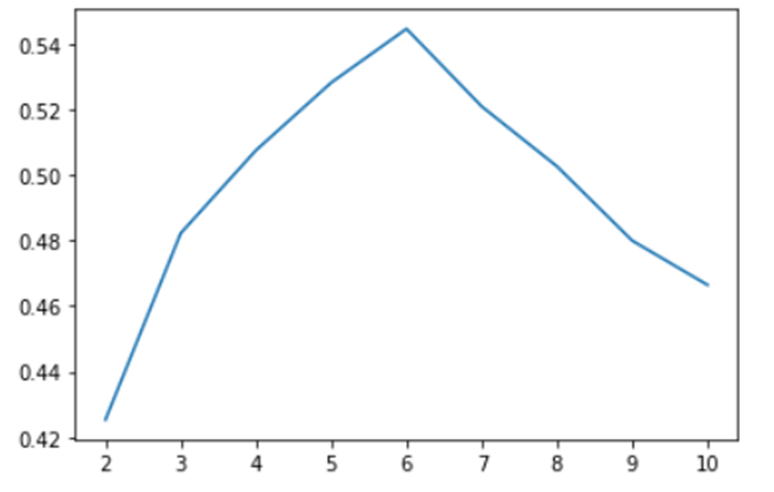
제일 점수가 높은 6일 때 군집이 잘 나눠졌다고 볼 수 있다.
하지만 점수가 높다고 또 가장 좋은 건 아닌 걸 확인할 수 있는데, 예를 들어보겠다. 다음과 같이 나왔기 때문에 최적의 k를 4로 해서 봤다.

4로 해서 봤더니 아래와 같이 군집이 나눠졌는데 육안으로 봤을 때는 동그라미처럼 더 많은 군집으로 나눠질 수 있을 것 같았다. 그래서 3번째로 값이 높지만 클러스터의 수가 더 많은 8로 지정해서 봤더니 오른쪽과 같은 그림이 나왔다. 이게 더 우리가 생각했을 때 잘 나눠진 군집이라 볼 수 있다.


그러니 꼭 최적의 k를 찾는데 위와 같은 2가지 방법을 신뢰할 순 없다. 더 많은 살을 붙여야 한다.
'개발 Tools > 파이썬_Deep learning & ML' 카테고리의 다른 글
| 딥러닝을 위한 기초 개념 Perceptron ( 활성함수, DNN ) (0) | 2022.05.04 |
|---|---|
| 딥러닝을 위한 기초 개념 Entropy ( Cross entropy, KL divergence, 엔트로피 ) (0) | 2022.05.02 |
| 머신러닝 Spectral Clustering (0) | 2022.02.11 |
| 머신러닝 fit_transform() 과 transform()의 차이점 (0) | 2021.12.12 |
| 딥러닝 LSTM (Long Short-Term Memory) (0) | 2021.10.22 |



댓글